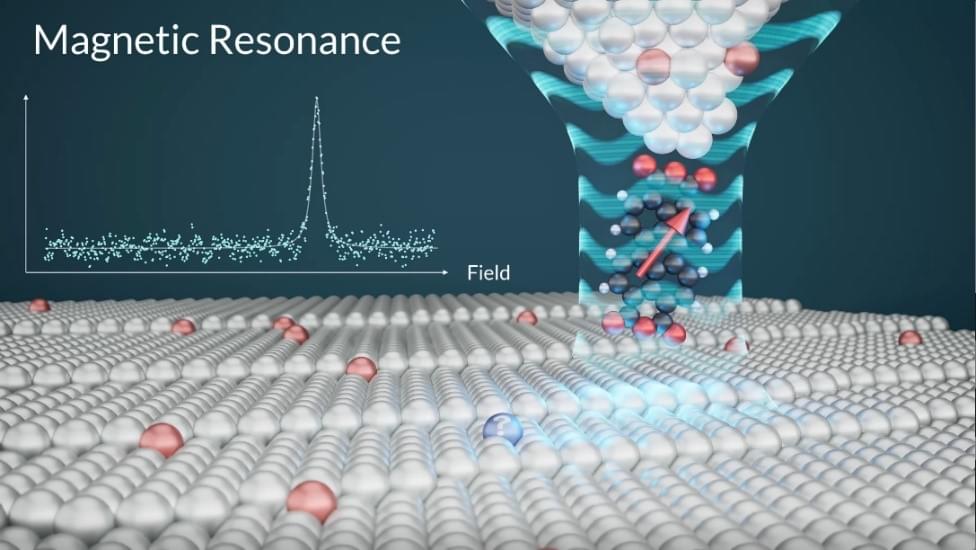
In a scientific breakthrough, an international research team from Korea’s IBS Center for Quantum Nanoscience (QNS) and Germany’s Forschungszentrum Jülich developed a quantum sensor capable of detecting minute magnetic fields at the atomic length scale. This pioneering work realizes a long-held dream of scientists: an MRI-like tool for quantum materials.
The research team utilized the expertise of bottom-up single-molecule fabrication from the Jülich group while conducting experiments at QNS, utilizing the Korean team’s leading-edge instrumentation and methodological know-how to develop the world’s first quantum sensor for the atomic world.
The diameter of an atom is a million times smaller than the thickest human hair. This makes it extremely challenging to visualize and precisely measure physical quantities like electric and magnetic fields emerging from atoms. To sense such weak fields from a single atom, the observing tool must be highly sensitive and as small as the atoms themselves.