Some Limits to Global Ecophagy by Biovorous Nanoreplicators, with Public Policy Recommendations

by Lifeboat Foundation Scientific Advisory Board member Robert A. Freitas Jr. Original paper is at his site.

Abstract

The maximum rate of global ecophagy by biovorous self-replicating nanorobots is fundamentally restricted by the replicative strategy employed; by the maximum dispersal velocity of mobile replicators; by operational energy and chemical element requirements; by the homeostatic resistance of biological ecologies to ecophagy; by ecophagic thermal pollution limits (ETPL); and most importantly by our determination and readiness to stop them.

Assuming current and foreseeable energy-dissipative designs requiring ~100 MJ/kg for chemical transformations (most likely for biovorous systems), ecophagy that proceeds slowly enough to add ~4°C to global warming (near the current threshold for immediate climatological detection) will require ~20 months to run to completion; faster ecophagic devices run hotter, allowing quicker detection by policing authorities. All ecophagic scenarios examined appear to permit early detection by vigilant monitoring, thus enabling rapid deployment of effective defensive instrumentalities.

1.0 Introduction

Recent discussions [1] of the possible dangers posed by future technologies such as artificial intelligence, genetic engineering and molecular nanotechnology have made it clear that an intensive theoretical analysis of the major classes of environmental risks of molecular nanotechnology (MNT) is warranted. No systematic assessment of the risks and limitations of MNT-based technologies has yet been attempted. This paper represents a first effort to begin this analytical process in a quantitative fashion.

Perhaps the earliest-recognized and best-known danger of molecular nanotechnology is the risk that self-replicating nanorobots capable of functioning autonomously in the natural environment could quickly convert that natural environment (e.g., “biomass”) into replicas of themselves (e.g., “nanomass”) on a global basis, a scenario usually referred to as the “gray goo problem” but perhaps more properly termed “global ecophagy”.

As Drexler first warned in Engines of Creation [2]:

“Plants” with “leaves” no more efficient than today’s solar cells could out-compete real plants, crowding the biosphere with an inedible foliage. Tough omnivorous “bacteria” could out-compete real bacteria: They could spread like blowing pollen, replicate swiftly, and reduce the biosphere to dust in a matter of days. Dangerous replicators could easily be too tough, small, and rapidly spreading to stop – at least if we make no preparation. We have trouble enough controlling viruses and fruit flies.

Among the cognoscenti of nanotechnology, this threat has become known as the “gray goo problem”. Though masses of uncontrolled replicators need not be gray or gooey, the term “gray goo” emphasizes that replicators able to obliterate life might be less inspiring than a single species of crabgrass. They might be superior in an evolutionary sense, but this need not make them valuable.

The gray goo threat makes one thing perfectly clear: We cannot afford certain kinds of accidents with replicating assemblers.

Gray goo would surely be a depressing ending to our human adventure on Earth, far worse than mere fire or ice, and one that could stem from a simple laboratory accident.

Lederberg [3] notes that the microbial world is evolving at a fast pace, and suggests that our survival may depend upon embracing a “more microbial point of view”. The emergence of new infectious agents such as HIV and Ebola demonstrates that we have as yet little knowledge of how natural or technological disruptions to the environment might trigger mutations in known organisms or unknown extant organisms [81], producing a limited form of “green goo” [92].

However, biovorous nanorobots capable of comprehensive ecophagy will not be easy to build and their design will require exquisite attention to numerous complex specifications and operational challenges. Such biovores can emerge only after a lengthy period of purposeful focused effort, or as a result of deliberate experiments aimed at creating general-purpose artificial life, perhaps by employing genetic algorithms, and are highly unlikely to arise solely by accident.

2.0 The Ecophagic Threat

Classical molecular nanotechnology [2, 4] envisions nanomachines predominantly composed of carbon-rich diamondoid materials. Other useful nanochemistries might employ aluminum-rich sapphire (Al₂O₃) materials, boron-rich (BN) or titanium-rich (TiC) materials, and the like. TiC has one the highest possible operating temperatures allowed for commonplace materials (m.p. ~3410°K [5]), and while diamond can scratch TiC, TiC can be used to melt diamond.

However, atoms of Al, Ti and B are far more abundant in the Earth’s crust (81,300 ppm, 4400 ppm, and 3 ppm, respectively [5]) than in biomass, e.g., the human body (0.1 ppm, 0 ppm, and 0.03 ppm [6]), reducing the direct threat of ecophagy by such systems (Section 8.3). On the other hand, carbon is a thousand times less abundant in crustal rocks (320 ppm, mostly carbonates) than in the biosphere (~230,000 ppm).

Furthermore, conversion of the lithosphere into nanomachinery is not a primary concern because ordinary rocks typically contain relatively scarce sources of energy. For instance, natural radioactive isotopes present in crustal rocks vary greatly as a function of the geological composition and history of a region, but generally range from 0.15–1.40 mGy/yr [7], giving a raw power density of 0.28–2.6 × 10^-7 W/m³ assuming crustal rocks of approximately mean terrestrial density (5522 kg/m³ [5]). This is quite insufficient to power nanorobots capable of significant activities; current nanomachine designs typically require power densities on the order of 10⁵–10⁹ W/m³ to achieve effective results [6]. (Biological systems typically operate at 10²–10⁶ W/m³ [6].) Solar power is not readily available below the surface, and the mean geothermal heat flow is only 0.05 W/m² at the surface [6], just a tiny fraction of solar insolation.

Subsurface pressure and temperature rise with depth in Earth’s crust at the rates of 0.47 atm/meter and k_q ~ 0.014°K/meter [8], exceeding maximum reasonable nanorobot operating limits of 100,000 atm and 2000°K at depths of ~210 km and ~120 km well into the upper mantle below a ~50 km crust; however, geothermal power density is only D_p ~ K_t k_q²k_Carnot / DT ~ 1–4 × 10^-6 W/m³ taking thermal conductivity K_t ~ 2–5 W/m-K for common crustal minerals [9] and DT ~ 1°C giving Carnot efficiency k_Carnot = DT / T ~ 0.3% at T = 300°K.

Hypothesized crustal abiotic highly-reduced petroleum reserves [16] probably could not energize significant replicator nanomass growth due to the anoxic environment deep underground, although potentially large geobacterial populations have been described [10–16] and in principle some unusual though highly limited bacterial energy sources could also be tapped by nanorobots.

For example, some anaerobic bacteria use metals (instead of oxygen) as electron-acceptors [13], with iron present in minerals such as pyroxene or olivine being converted to iron in a more oxidized state in magnetic minerals such as magnetite and maghemite, and using geochemically produced hydrogen to reduce CO₂ to methane [11]. Underground bacteria in the Antrim Shale deposit produce 1.2 × 10⁷ m³/day of natural gas (methane) by consuming the 370 MY-old remains of ancient algae [17]. Bioremediation experiments have also been done by Envirogen and others in which pollution-eating bacteria are purposely injected into the ground to metabolize organic toxins; in field tests it has proven difficult to get the bacteria to move through underground aquifers, because the negatively-charged cells tend to adhere to positively charged iron oxides in the soil [18].

However, the primary ecophagic concern is that runaway nanorobotic replicators or “replibots” will convert the entire surface biosphere (the ecology of all living things on the surface of the Earth) into alternative or artificial materials of some type — especially, materials like themselves, e.g., more self-replicating nanorobots.

Since advanced nanorobots might be constructed predominantly of carbon-rich diamondoid materials [4], and since ~12% of all atoms in the human body (representative of biology generally) are carbon atoms [6], or ~23% by weight, the global biological carbon inventory may support the self-manufacture of a final mass of replicating diamondoid nanorobots on the order of ~0.23 M_bio, where M_bio is the total global biomass.

Unlike almost any other natural material, biomass can serve both as a source of carbon and as a source of power for nanomachine replication. Ecophagic nanorobots would regard living things as environmental carbon accumulators, and biomass as a valuable ore to be mined for carbon and energy. Of course, biosystems from which all carbon has been extracted can no longer be alive but would instead become lifeless chemical sludge.

3.0 Exponential Replication

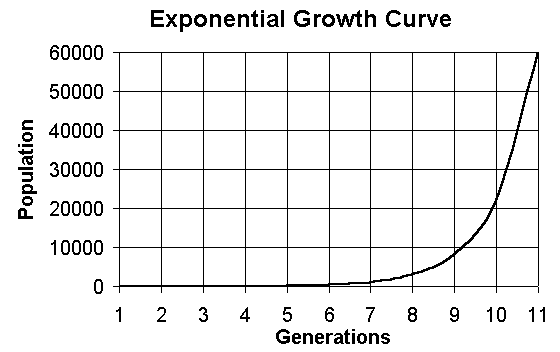
The power of exponential replication.
Ignoring thermal pollution considerations for the moment (Section 6.0), in theory an optimally designed and geographically uniformly distributed population of replibots could increase the mass of their own population at the expense of the biosphere, via self-replication, according to the simple relation [19]:

M_repl = M_inite^(t/t)

(1)

for maximum exponential growth, where t is elapsed time (sec), t is generation cycle or replication time (sec), M_init (kg) is initial nanorobot mass at time t = 0, and M_repl (kg) is the replicator mass at time t, where M_repl ≤ 0.23 M_bio. In order to achieve this rate, each completed component of the unit currently being built must be put to full productive use immediately, instead of waiting for the final completion of the unit.

There are a few design configurations where something close to this can be achieved efficiently, but as a practical matter and to retain simplicity it will usually be preferable to await the completion of a unit before pressing it into replicative service, a mode of operation called discrete replication, in which case the exponential term in Eqn. 1 should be replaced with 2^(t/tdiscrete⁾ — which, all else equal, will be a slightly slower function. (Discrete replication can be faster than pure exponential replication only if t_discrete < t ln(2).) Replicating populations limited to activity only at the perimeter of the expansion wave, or in regions of high replibot number density, may achieve only polynomial growth rates [19], which are even slower.

In order to estimate t = t_conv, the time required for total conversion of the biosphere to replibots plus waste sludge, we must first estimate t. Drexler [4] has calculated that a readily-envisioned multistage molecular manufacturing system could manufacture its own mass in t ~ 1000 seconds. However, nanoreplicators need not be capable of general purpose manufacturing, but may be optimized solely for replication of their own substance.

A molecular manipulator designed by Drexler [4] that is suitable for molecular assembly pick-and-place operations consists of 4 million atoms excluding support base, power, control, and other necessary structures, and is designed to perform ~10⁶ atomic-precision molecular pick-and-place operations per second, assuming arm-tip movement at 1 cm/sec over minimal 10-nm arcs each cycle. Freitas [6] estimates that a basic autonomous nanoassembler using two Drexler manipulator arms and incorporating a simple onboard nanocomputer might require at least ~70 million atoms (~1 gigadalton), suggesting a minimum replication time t ~ 100 seconds. (The smallest independently viable cells are thought to have a molecular weight of order ~1 gigadalton, e.g., minimum diameter ~140 nm[72, 73].)

It is difficult to imagine how an ecophagic replicator capable of successfully assimilating natural biomatter of all existing varieties could be much simpler than this. However, it is possible that molecular manipulators might be slewed at speeds up to ~100 cm/sec, perhaps giving t ~ 1 sec, but at the cost of steeply rising energy dissipation [4] which greatly increases waste heat production and system operating temperatures, and reduces nanoreplicator reliability due to larger thermally-excited displacements, thermal damage rates, and phonon-mediated drag [4]. For example, a 10-nm force sensor measuring 10 pN at an operating temperature of 300°K has a 0.2% probability of erroneous measurement; this probability jumps to 3% at 500°K and 16% at 1000°K [4]. Hence, t ~ 1 sec appears to be a rather aggressive and probably unachievable lower limit.

Table 1. Terrestrial Carbon Sources
Location of the Carbon	Form of the Carbon	Worldwide Quantity of Carbon
Biosphere	CHON ^a	1.1 × 10¹⁵ kg
Atmosphere	CO₂, CH₄^b	5.2 × 10¹⁴ kg
Hydrosphere	CO₂^c	3.8 × 10¹⁶ kg
	CH₄^d	1–2 × 10¹⁶ kg
Lithosphere	Petroleum ^e	1–3 × 10¹⁴ kg
	Coal ^f	1–2 × 10¹⁶ kg
	Carbonates ^g	~1 × 10¹⁹ kg

estimated carbon inventory in the global biomass [20, 21]
atmospheric carbon inventory, mostly CO₂ at 362 ppm [22] and CH₄ at 1.7 ppm [46]
total ocean-dissolved carbon as CO₂, assuming a mean concentration of 2300 micromoles CO₂ per kg of seawater [26] and an ocean mass of 1.36 × 10²¹ kg [6]
global undersea carbon storage on continental margins as CH₄ gas hydrates and gas trapped beneath [24]
Earth’s total original underground petroleum endowment was 2–4 × 10¹⁴ kg, of which ~1 × 10¹⁴ kg has already been consumed [23]
all identified and undiscovered global coal reserves [25]
assumes 320 ppm C in crustal rocks [5] to ~50 km depth

Carbon inventory in the global biomass has been estimated as 1.1 × 10¹⁵ kg (Table 1). Life is ~23% carbon by weight, so the total global biomass can be estimated as M_bio ~ 5 × 10¹⁵ kg. Starting from a single 70-million-atom replicator of mass ~1 gigadalton [6] or M_init ~ 1.7 × 10^-18 kg, and taking t ~ 1 sec and M_repl = 0.23 M_bio ~ 1.2 × 10¹⁵ kg, then t_conv ~ 76 sec. Adopting a more reasonable t ~ 100 sec, t_conv ~ 7600 sec. For comparison, the fastest known replicators found in nature are certain bacteria which have a mean generation time of t ~ 900–1200 sec (15–20 minutes) [27]. However, these bacteria are capable of digesting only certain limited forms of biological matter and have very severe operational restrictions including proper temperature, pH, and so forth. They are not bio-omnivorous.

4.0 Dispersal Velocity Limitation

The expansion of any population of replicating systems is also fundamentally restricted by the expansion velocity of the outermost envelope which defines the maximum physical extent or dispersion of the growing population. No population of ecophagic objects can disperse more quickly than its growth medium — in this case, the terrestrial biosphere — will permit. Thus for a two-dimensional growth medium on the surface of a sphere (e.g., the Earth), the time required for complete biospheric conversion starting from a single initial release site must be at least the minimum time required for the replibots to travel exactly half of a great circle route across the spherical surface, since the expanding wavefront of conversion is moving around the globe in all compass directions simultaneously. This minimum conversion time may be crudely approximated as:

t_spread ³ v_repl^-1 (4pR_Earth² / N)^½

(2)

assuming t_spread > t, where the mean planetary radius R_Earth = 6.37 × 10⁶ meters, N is the number of initial replibot release sites, and v_repl is the maximum nanoreplicator linear dispersal velocity. For isolated replibots lacking significant aeromotive capabilities, dispersal velocity will be limited approximately to the mean global wind speed, perhaps v_repl ~ 10 m/sec, ignoring the narrow 30–75 m/sec jet streams at 9–16 km altitude [94]. This is also near the maximum feasible velocity for nanorobotic flyers operating in the viscous regime, based on maximum attainable endogenous power densities [6].

Assuming a single initial release site (N = 1) and taking v_repl ~ 10 m/sec, then t_spread ~ 2 × 10⁶ sec. However, a more efficient biosphere conversion strategy would incorporate the simultaneous release of numerous “seed” replibots distributed uniformly throughout the terrestrial biomass, thus reducing the required maximum extension of each expanding replication domain from neighboring replibot release sites.

Large numbers of replibots could be transported by high-velocity airborne macroscale carrier vehicles to distant sites around the world and then released, crudely analogous to a jet aircraft scattering printed leaflets over a civilian area during wartime. Nanoreplicator progeny tasked with the conversion of biomass to nanomass within such smaller substrate domains have much less distance to travel to complete their purpose. Minimum biomass conversion time scales roughly as N^½, where N is the number of independent initial replicator domains, as reflected in Table 2 generated from Eqn. 2:

Table 2. Minimum Replibot Dispersal Time as a Function of the Number of Uniformly-Distributed Replibot Release Sites
# of Release Sites (N)	Mean Distance Between Neighboring Release Site	Min. Global Dispersal Time, t_spread (for v_repl = 10 m/sec)
1	2 × 10⁷ meters	30 days
10²	2 × 10⁶ meters	3 days
10⁴	2 × 10⁵ meters	6 hours
10⁶	2 × 10⁴ meters	40 minutes
10⁸	2 × 10³ meters	200 sec
10¹⁰	2 × 10² meters	20 sec
10¹²	2 × 10¹ meters	2 sec

This analysis suggests that the limitations on biosphere conversion rate imposed by dispersal velocity are readily overcome by employing a sufficient number of release sites, and do not, by themselves, prohibit ecophagic conversion times on the order of ~1000 seconds or less. In principle, very sophisticated biovores could facultatively aggregate into macroscale assemblages to escape the viscous flight regime, theoretically permitting aerodynamic or even suborbital flight velocities up to 100–1000 m/sec. Replicators incapable of aerial transport will experience significantly longer dispersal times.

In practical surface deployments, major distribution nonuniformities will exist because some areas have significantly larger carbon inventories than others [28]. For example, a map of the global annual net primary production (NPP) of photosynthetically fixed carbon on land shows NPP ranging from 0.1–1.5 kg/m²-yr of carbon, with 25% of the land surface area without permanent ice supporting an NPP > 0.5 kg/m²-yr and an average of 0.426 kg/m²-yr on land [21]. The oceans, which cover ~70% of Earth’s surface and show carbon fixation activity averaging only 0.14 kg/m²-yr [21], contain a mere 0.02% of the entire planetary biomass, compared to 99.98% on land.

The uneven geographical distribution of carbon inventories [28] and solar power availability [83] along with possible element shortages (Tables 3 and 5) may produce significant geographical variation in replication rates. A detailed analysis of such variation is beyond the scope of this paper but likely would place upper limits on replication speed in many environments.

5.0 Energy and Materials Requirements Limitations

The need for energy is another fundamental limit on the speed at which biospheric conversion can take place. During ecophagy, the richest source of energy is likely to be chemical energy derived from the assimilation of biomolecules found in the biosphere. For example, a biomass density of ~10 kg/m² on land [20, 21] typically having ~10⁷ J/kg of recoverable chemical energy [6] implies an available energy density of ~10⁸ J/m² at the terrestrial surface.

By comparison, visible-spectrum sunlight at noon on a cloudless day (I_solar ~ 100–400 W/m² [6]) may provide at most ~10⁷ J/m² over the course of an 8-hour work day. Other sources of scavengable energy such as radionuclides are much scarcer (Section 2.0). Note that the complete combustion in air of a mass of glucose equal to M_bio would consume ~5.3 × 10¹⁵ kg O₂, only 0.5% of the ~1.1 × 10¹⁸ kg of oxygen contained within Earth’s ~21% O₂ atmosphere. Hence oxygen-dependent ecophagy will not be oxygen-limited.

Interestingly, diamond has the highest known oxidative chemical storage density because it has the highest atom number (and bond) density per unit volume. Organic materials store less energy per unit volume, from ~3 times less than diamond for cholesterol, to ~5 times less for vegetable protein, to ~10–12 times less for amino acids and wood [6].

Since replibots must build energy-rich product structures (e.g. diamondoid) by consuming relatively energy-poor feedstock structures (e.g., biomass), it may not be possible for biosphere conversion to proceed entirely to completion (e.g., all carbon atoms incorporated into nanorobots) using chemical energy alone, even taking into account the possible energy value of the decarbonified sludge byproduct, though such unused carbon may enter the atmosphere as CO₂ and will still be lost to the biosphere.

The speed of biospheric conversion can also be limited by the abundances of chemical elements available in the environment for conversion into nanomass, as compared to the relative quantities of each element that are required by the nanorobot for replication. (In replicator engineering, this is the “materials closure” issue [19]; in chemistry, it is called “stoichiometry”.)

In the gray goo scenario, nanorobot replication occurs on the Earth’s surface, so any elements which are in short supply in the biosphere might alternatively be obtained from nearby topsoil or crustal rocks, although this may impose an additional logistical overhead on replicative processes. Hence only the concentration of the most abundant of these two sources may act as a significant limit to replication speed. Traditional diamondoid nanomachinery designs [4] have employed 8 primary chemical elements, as summarized in Table 3 (more details in Table 5); Table 3 also gives the associated biological [6] and crustal [5] abundances for each element.

Table 3. Chemical Element Usages by Weight in Classical Diamondoid Nanorobot Designs Compared to Biological and Terrestrial Crustal Chemical Element Abundances
Chemical Element	% by Wt. in Nanorobot Designs	% by Wt. in Human Body (biology)	% by Wt. in Earth’s Crust	Range of t_mult
O	3.95% – 7.20%	61.1%	46.6%	1
H	0.58% – 1.35%	10.01%	0.14%	1
Si	4.13% – 52.60%	0.0259%	27.7%	1 – 2
C	19.87% – 57.71%	22.9%	0.032%	1 – 3
P	0% – 9.43%	0.706%	0.118%	0 – 13
N	3.56% – 25.19%	1.30%	0.0046%	3 – 19
F	0% – 0.77%	0.00374%	0.030%	0 – 26
S	3.65% – 7.98%	0.197%	0.052%	19 – 41

Dividing the lowest and highest nanorobot requirement by the highest available environmental abundance gives t_mult, the required increase in replication time due to scarcity of a chemical element required for replication. Inspection of Table 3 reveals that sulfur appears to be in the shortest supply relative to nanorobot requirements (at least for current primitive designs), possibly increasing replication time t by a factor of up to 41 while the device waits for sufficient sulfur atoms to be accumulated from the environment. Other elements possibly in somewhat limited supply include P, N and F, although the impact of any of these elements on replication time can probably be minimized by judicious nanorobot composition design choices.

As a general rule, ecophagic nanorobot replication time is longer in direct proportion to the extent that nanorobot elemental requirements exceed the availability of the scarcest element in the consumable substrate, in comparison to the theoretical nanorobot replication time on a perfectly compositionally-matched substrate [19]. This phenomenon is commonplace in biology. For instance, it is well-known that phytoplanktonic growth in the open oceans is iron-limited [29].

The highest near-term risk could come from relatively simple single-behavior replibots whose niche is a high-energy substrate of uniform composition which affords a rapid vector for the dispersal of the replicators [79].

The classic example is tire rubber and asphalt tar binder; cars, trucks and airplanes roll on roads and tarmacs worldwide. If the ~4 million miles of paved roads in the U.S. [80] represent ~25% of the global total, then road asphalt mass worldwide is ~3 × 10¹³ kg, or ~0.6% M_bio; the global rubber tire population of ~10 billion tires stockpiled, in use or discarded in scrap heaps [80, 82] adds another ~0.003% M_bio. Other vectors with similar properties include cotton, polyester or other uniform textiles [79], insulation on electrical wiring, and paper money. Regular monitoring and decontamination procedures may thwart these threats.

6.0 Ecophagic Thermal Pollution Limits (ETPL)

A more restrictive limitation on the maximum speed of biomass conversion to nanomass is the generation and release of process waste heat into the environment during ecophagy. If there are too many nanoreplicators working all at once, the waste heat they generate can begin to warm up the environment. In some cases, the environment could become so hot that the biospheric conversion process can no longer proceed.

In the crude analysis that follows, we assume that after some number of prior replication cycles, the replibots have converted roughly half of the biosphere to nanoreplicator mass. In the next and final replication cycle, the energy extractable from the remaining half of the global biomass will be consumed as each existing nanorobot replicates itself once more for the last time, thus promptly doubling the existing population and completing the global conversion of biomass into nanomass.

In this case, the total heat energy released at Earth’s surface is P_total = P_nano + P_solar, where P_nano is the waste heat generated by the replibots as they emit E_half joules in the last replicative cycle of duration t_last, with P_nano = E_half / t_last, and where the total solar insolation on Earth’s cloudless surface that is subsequently thermalized is P_solar ~ 1.75 × 10¹⁷ W. Neglecting the heat-trapping effects of greenhouse gases and the minor contributions from the geological heat flow at Earth’s surface, the temperature at the terrestrial surface is given approximately by the Stefan-Boltzmann relation:

P_total = 4pR_Earth²e_rsT_Earth⁴

(3)

where e_r is terrestrial surface emissivity, taken here as 0.97 (e.g. carbon black) to maximize heat emission at the lowest possible temperature, s is the Stefan-Boltzmann constant (5.67 × 10^-8 W/m²-K⁴), and T_Earth is the mean surface temperature of Earth. The minimum last-replication time that will allow a global temperature of T_Earth or lower to be maintained throughout the final conversion cycle is given by:

t_last = E_half / [4 pR_Earth²e_rsT_Earth⁴–P_solar]	(4)

~ E_half / [ (2.8 × 10⁷) T_Earth⁴– (1.75 × 10¹⁷) ]

What is an appropriate maximum operating temperature limit for nanoreplicators that must forage for organic substrate in order to replicate? The softening point for sapphire, an oft-mentioned substitute building material for diamond because of its high strength, high-temperature tolerance, and inability to burn in oxygen, is 2070°K [30], probably near the upper limit in any reasonable ecophagic nanorobot design scenario especially given the seriously negative impact of higher temperatures on nanorobot reliability and functionality (Section 3.0). The combustion temperature of diamond in air is usually given as 870–1070°K [31].

However, such elevated surface temperatures, while perhaps acceptable for diamondoid nanomachines in some circumstances, will immediately volatize and incinerate most of the natural organic feedstock upon which the nanoreplicators must feed.

The minimum ignition point of wood, paper, or diesel fuel in air has been given as low as ~500°K [68], and glucose caramelizes [6] at 433°K — caramelization is not oxidation but rather is a decomposition reaction that includes polymerizations and covalent bondmaking that could render this substrate material somewhat less accessible to the replibots.

A still lower temperature threshold is the boiling point of water at 373°K; above this temperature, living things will boil, thus denying ecophagic nanoreplicators access to solution-based chemical processes at normal atmospheric pressures, which could be an important restriction.

The waste heat energy released globally in the last replicative cycle may be estimated as E_half ≤ (q D_bio) M_bio, where D_bio is the energy density of the organic feedstock material and q is the energy conversion ratio for its transformation into nanomass. For example, D_bio = 16 MJ/kg for glucose, 17 MJ/kg for vegetable protein, 18 MJ/kg for animal protein, 19 MJ/kg for wood, and 39 MJ/kg for fats [6]. However, these figures refer to the energy content of the organic feedstock, not to the energy that must be consumed (and the waste heat subsequently thermalized) in order to build a kilogram of nanomass.

Drexler [4] estimates that the typical energy dissipation caused by chemical transformations involving carbon-rich materials will be E_diss = (q D_bio) ~ 100 MJ/kg of final product using readily-envisioned irreversible methods in systems where low energy dissipation is not a primary design objective. This figure corresponds roughly to the strongest covalent bond energies (e.g., 1190 zJ/bond for C=C, 1327 zJ/bond for C=O, and 1594 zJ/bond for CºC [4]), and is roughly of the same order as the thermodynamic heat of formation of diamond from CO₂(g), ~33 MJ/kg [5].

Drexler [4] claims that energy dissipation may in theory be as low as E_diss ~ 0.1 MJ/kg “if one assumes the development of a set of mechanochemical processes capable of transforming feedstock molecules into complex product structures using only reliable, nearly reversible steps.” 0.1 MJ/kg of diamond corresponds roughly to the minimum thermal noise at room temperature (e.g., kT ~ 4 zJ/atom at 298°K).

R. Merkle [32] also conjectures that near-zero energy dissipation is in principle possible in certain special circumstances, a possibility that should be investigated in the present context in a future theoretical study. However, near-term nanochemistries are unlikely to be significantly more efficient than natural enzyme chemistries, which have been evolving for efficiency over eons; the terrestrial biosphere fixes ~1.2 × 10¹⁴ kg/yr of biomass carbon [21] with a ~1.4 × 10¹⁴ watt energy input [6], or E_diss ~ 38 MJ/kg of carbon.

Using Eqn. 4, the minimum last-replication time can be calculated for various plausible values of E_diss, wherein the mean terrestrial temperature will not exceed the chosen value of T_Earth during ecophagy, as given in Table 4:

Table 4. Minimum Last-Cycle Replication Time for Ecophagic Nanorobots as a Function of Replication Energy Efficiency and the Resulting Global Temperature
Mean Terrestrial Temperature (T_Earth)	Min. Last-Cycle Replication Time t_last (sec) for E_diss =
Mean Terrestrial Temperature (T_Earth)	0.1 MJ/kg	1.0 MJ/kg	10. MJ/kg	100 MJ/kg
281°K	¥	¥	¥	¥
285°K	5 × 10⁴	5 × 10⁵	5 × 10⁶	5 × 10⁷
300°K	1 × 10⁴	1 × 10⁵	1 × 10⁶	1 × 10⁷
320°K	4 × 10³	4 × 10⁴	4 × 10⁵	4 × 10⁶
373°K	1 × 10³	1 × 10⁴	1 × 10⁵	1 × 10⁶
400°K	9 × 10²	9 × 10³	9 × 10⁴	9 × 10⁵
500°K	3 × 10²	3 × 10³	3 × 10⁴	3 × 10⁵
1000°K	2 × 10^{1 *}	2 × 10²	2 × 10³	2 × 10⁴
2000°K	1 × 10^{0 *}	1 × 10^{1 *}	1 × 10²	1 × 10³
5000°K	3 × 10^{-2 *}	3 × 10^{-1 *}	3 × 10^{0 *}	3 × 10^{1 *}

^*Actual last-cycle replication time limited to exponential t ~ 100 sec (Section 3.0).

Setting aside Merkle’s conjecture, Table 4 suggests that if phenomenally efficient reversible molecular manufacturing techniques become available — e.g., E_diss ~ 0.1 MJ/kg — the final replicative cycle of global ecophagy could proceed as quickly as ~1000 seconds while just avoiding incinerating the organic feedstock or boiling environmental water. However, there currently exist no known designs which would be capable of achieving such highly energy-efficient nanoassembly operations.

More probably, highly dissipative molecular manufacturing designs are likely to be implemented during the early and intermediate years of molecular nanotechnology development. Such designs are also likely to be necessary for the very complex machines needed to implement biovorous replication given the enormous variety of chemically diverse natural biological substrates.

Assuming current and foreseeable energy-dissipative designs requiring ~100 MJ/kg for chemical transformations (most likely for biovorous systems), complete ecophagy that proceeds slowly enough to add ~4°C to global warming (near the current threshold for immediate climatological detection) will require ~20 months to run to completion. Faster ecophagic devices will run hotter, allowing quicker detection by policing authorities.

The conversion of biomass to nanomass may proceed according to Eqn. 1 up to the ecophagic thermal pollution limit (ETPL) whereupon the specified maximum global temperature T_Earth is attained, after which the replication time must approximately double after each population doubling, ultimately reaching t_last in the final doubling, as described by Eqn. 4. Total time spent in the ETPL-limited regime is ~ 2 t_last.

For example, taking t = 100 sec, T_Earth = 300°K, and E_diss ~ 100 MJ/kg, the transition to the ETPL regime occurs when total global nanomass reaches ~5 × 10¹⁰ kg, or only 0.001% of total global biomass, and the last ~17 population doublings remain to be completed over a time span of ~2 t_last = 2 × 10⁷ sec (~7 months). This is also the optimum strategy for an ecophagic population that is attempting to evade premature detection by maintaining a low thermal emissions profile. Constant ecological surveillance for any evidence of ecophagic activity is an appropriate policing measure to provide adequate early warning to the existence of this threat.

Note further that the presence of natural and anthropogenic greenhouse gases in the Earth’s atmosphere will amplify any heating effects, helping to make ecophagic activities more immediately visible in its earlier stages. (In theory, a large enough replibot population could actively manage terrestrial albedo or global greenhouse gas concentrations, but these activities would themselves generate still more waste heat.)

Additionally, using the actual current mean value of e_r = 0.69 for terrestrial emissivity in Eqns. 3 and 4, rather than the much higher value of e_r = 0.97 for carbon black assumed in calculating Table 4, the last-cycle time t_last increases by another ~40%, giving still more time for defensive instrumentalities to be brought to bear on the situation.

Assuming the surface biomass is compositionally similar to wood (D_bio ~ 19 MJ/kg), prompt consumption (e.g., combustion) of the entire biosphere would release Q_waste = M_bioD_bio ~ 10²³ J of energy. The combined heat capacity of planetary oceans (1.36 × 10²¹ kg [6] at 4200 J/kg-K [6] = 6 × 10²⁴ J/K) and land (~4 × 10²⁰ kg/km crustal landmass at, e.g., 833 J/kg-K for silica [90] = 3 × 10²³ J/km-K) is ~10²⁵ J/K, so in principle Q_waste, ideally distributed, could be absorbed with a negligible rise in global temperature, ~0.01ºK — although even a slight rise in ocean temperature could increase mean worldwide humidity, greatly amplifying global warming because water vapor is the most effective greenhouse gas [91].

However, in the instant scenario, the replibots are assumed to be in intimate contact with the biomass which they are consuming — not with the vast volumes of sea or land. Air is an excellent insulator (see below), and the thermal conductivity of wood is ~4 times higher than for air, so replication waste heat energy will be conducted primarily into the nanorobot population and the proximate biomass that is being consumed. The heat capacity of diamond and organic materials (e.g. wood, rubber, etc.) is ~2 MJ/m³-K [6], or ~800 J/kg-K for the biomass/nanomass aggregate as dry mass or up to 3200 J/kg-K assuming 70% water content.

Taking the higher figure, the total heat capacity of the biomass/nanomass aggregate is C_bn ~ 3200 J/kg-K × M_bio = 2 × 10¹⁹ J/K. Adding Q_waste to this aggregate would raise its temperature by DT ~ Q_waste / C_bn ~ 5,000ºK.

Similarly, air conduction is unlikely to significantly reduce the ETPL limits. Waste energy can be absorbed by atmospheric heat capacity (5.27 × 10¹⁸ kg [6] at 988 J/kg-K [6] = 5 × 10²¹ J/K) only if said heat energy is delivered to the atmosphere and thoroughly mixed via conduction, convection, or radiative transfer. But the thermal conductivity (K_t) of air is very poor.

Consider a layer of air H meters thick and area A, with temperature differential DT on opposite faces, with power flow through the layer of P = K_t ADT / H = Q_waste / t_burn, where power is generated by consuming the ecosphere in a time t_burn, so the temperature differential across the layer is DT = Q_waste H / (K_t At_burn). With a thin layer of replibots coating the foliage on Earth’s surface, generating heat only on the “skin” of the biosphere, there will be a nonconvective stagnant layer of air trapped for long periods near the surface that is poorly mixed by winds.

In weather modeling this viscous sublayer, called the roughness parameter, may be ~0.01–300 cm thick [84–86] (e.g., 0.01 cm over water surface, 0.1 cm over short grain, 10 cm over prairie grass, 100 cm over grain crops [85]), and sometimes is taken as ~10% of the height of the obstacle [87]. Assuming H ~ 1 cm layer and taking Q_waste = 10²³ J, K_t = 2.5 × 10^-2 W/m-K for air [6], A = 5.10 × 10¹⁴ m² for Earth, then DT ~ 7 × 10⁷ / t_burn.

Thus, consuming M_bio in t_burn = 10⁴ sec nominally produces a temperature differential across the 1 cm layer of DT ~ 7000ºK (and violates our nonconvection assumption); assuming t_burn = 6 months, then DT ~ 4ºK, detectable using current orbital surveillance assets given a normal tropospheric thermal gradient of 0.006–0.009ºK/m [88].] (Vertical temperature gradients below 0.010ºK/m are considered subadiabatic, producing downward buoyancy forces [89].)

These crude estimates provide an approximate indication of the magnitudes involved, but the details of convective vertical mixing and its possible meteorological consequences during ecophagy are beyond the scope of this paper and should be investigated further.

7.0 Homeostatic Resistance to Ecophagy Thermal Pollution Limits (ETPL)

Over long time periods, natural ecosystems are believed to have a nearly balanced carbon budget, with photosynthetic uptake equal to respiratory release [33]. From the ecological perspective, the insertion of carbon-absorbing artificial devices into the environment represents a new sink in the homeostatic global carbon cycle, in addition to the natural carbon sinks such as forests [34, 35].

Most of terrestrial biomass consists of plants, especially trees, though nearly half of all biomass may consist of bacteria, mostly in soils (up to ~10¹⁵ cells/m³) and subsurface sediments and rocks down to ~3 km depth [12, 38]; there are ~5 × 10³⁰ bacteria on Earth [39]. Conversion of living plant biomass to diamondoid nanomass by nanoreplicators thus may reduce the ability of the surviving plant population to remove carbon dioxide from the atmosphere.

Unless carbon dioxide levels in the atmosphere are directly regulated by the active robotic nanomass, CO₂ levels will begin to rise, which in turn may increase the growth rate of plants. In a few experimental studies [40], elevated CO₂ has been shown to stimulate plant growth at least temporarily, even under serious nutrient shortage, although one experiment [41] challenges this supposition. If slow-moving nanoreplicators consume biomass only very slowly, the consumed biomass may be regenerated as new plant growth is stimulated worldwide.

What is the minimum ecophagic biomass removal rate necessary to overcome the resulting carbon-sequestration response of the natural ecology?

One study [20] found that deforestation in the low latitudes during 1990 resulted in forest area expansion and growth in mid- and high-latitude forest that sequestered ~7 × 10¹¹ kg of carbon (e.g., creating ~3 × 10¹² kg of extra biomass) in one year. Estimates of unrealized global forest carbon conservation and sequestration potential suggest a biologic capability of 1–3 × 10¹² kg/yr (e.g., 4–13 × 10¹² kg/yr of biomass) for more than a century [20]. Global oceans are believed to absorb ~2 × 10¹² kg/yr of anthropogenically-produced carbon, creating ~9 × 10¹² kg of new biomass per year [20]. This gives a worldwide carbon sink of ~5 × 10¹² kg/yr of carbon [42] and thus a global biomass recovery of at least ~2 × 10¹³ kg/yr.

The upper limit is probably closer to the global net primary biomass production of ~5 × 10¹⁴ kg/yr [21]. (Indeed, natural variations of ~10¹⁴ kg of atmospheric carbon (equivalent to ~6 × 10¹⁴ kg of biomass) were recorded over a ~600-year period during the last three glaciation cycles [43].) Thus it appears that a long-term ecophagic biomass removal rate exceeding 0.2–5 × 10¹⁴ kg/yr (~0.4%–10%/yr of the global biomass) may be necessary to overpower the natural ecological restorative forces.

8.0 Additional Scenarios

Four related scenarios which may lead indirectly to global ecophagy have been identified and are described below. In all cases, early detection appears feasible with advance preparation, and adequate defenses are readily conceived using molecular nanotechnologies of comparable sophistication.

8.1 Gray Plankton

Location of natural plankton (dark blue is where it is least concentrated).
The existence of 1–2 × 10¹⁶ kg [24] of global undersea carbon storage on continental margins as CH₄ clathrates and a like amount (3.8 × 10¹⁶ kg) of seawater-dissolved carbon as CO₂ represent a carbon inventory more than an order of magnitude larger than in the global biomass (Section 3.0).

Methane and CO₂ can in principle be combined to form free carbon and water, plus 0.5 MJ/kg C of free energy. (Some researchers are studying the possibility of reducing greenhouse gas accumulations by storing liquid [44] or solid [45] CO₂ on the ocean floor, which could potentially enable seabed replibots to more easily metabolize methane sources.)

Oxygen could also be imported from the surface in pressurized microtanks via buoyancy transport, with the conversion of carbon clathrates to nanomass taking place on the seabed below. The subsequent colonization of the land-based carbon-rich ecology by a large and hungry seabed-grown replicator population is the “gray plankton” scenario. (Phytoplankton, 1–200 microns in size, are the particles most responsible for the variable optical properties of oceanic water because of the strong absorption of these cells in the blue and red portions of the optical spectrum [37].)

The gray plankton replicator waste heat signature is readily detected at an early stage. The temperature of most of the ocean is near ~4°C — for example, ~1.6°C at 3627 m on the floor of Monterey Bay [44]. Typical ocean column thermal gradients are ~0.02°K/m in the top 300 m (1–30 atm) and ~0.006°K/m from 300–1000 m depth (30–100 atm) [44].

A near-seafloor water temperature change of DT = 1°K over a depth range of L = 100 m would be clearly distinguishable from natural variations even using contemporary instrumentation [44], and would evidence an increased seabed power release of I_repl ~ K_t (DT / L) ~ 0.005 W/m², taking thermal conductivity as K_t ~ 0.5 W/m-K for seawater at 4°C.

Thus the threshold for seafloor replibot detectability, assuming global seabed area is A_seabed ~ (70%) 4p R_Earth² = 3.6 × 10¹⁴ m², is P_min = I_repl A_seabed ~ 2 × 10¹² watts worldwide or a global replibot population of mass M_min ~ P_mint / E_diss ~ 20 × 10⁶ kg assuming E_diss ~ 100 MJ/kg and t = 1000 sec. (Faster replicators are detectable at lower population masses.) Thus bottom-dwelling gray plankton can be detected before they have consumed more than 10^-9 of the total oceanic abiotic carbon supply.

Direct census sampling of the seafloor may also allow early detection, although nanorobotic samplers will have to contend with a significant number of false targets in the oceanic environment. These false targets may include 0.1 micron small colloids (~7 × 10¹⁴ m^-3) and viruses (~3 × 10¹³ m^-3), 0.2–0.3 micron heterotrophic bacteria (~10¹² m^-3), 0.3 micron large colloids (~10¹³ m^-3), 1 micron cyanobacteria (~10¹⁰ m^-3), 2–3 micron small phytoplankton (~10⁸ m^-3), larger phytoplankton (e.g., 10 micron cells ~10⁶ m^-3), and zooplankton (e.g., 50 micron cells ~10³ m^-3) [36–38].

At the minimum detectable global mass of M_min = 20 × 10⁶ kg estimated above, the number density of gray plankton on the seabed floor is N_gp ~ M_min / (A_seabedm_gp) ~ 2 × 10⁷ m^-2, assuming ~1 micron gray plankton replicators each of mass m_gp ~ 3 × 10^-15 kg. In this scenario, the bottommost 1 mm of the ocean column above the seabed would contain roughly equal numbers of > ~1-micron natural cells and ~1-micron artificial bottom-dwelling gray plankton devices.

If not largely confined to the sea floor during most of their replication cycle, the natural cell/device ratio could increase by many orders of magnitude, requiring a more diligent census effort. Census-taking nanorobots can alternatively be used to identify, disable, knapsack or destroy the gray plankton devices.

8.2 Gray Dust (Aerovores)

Aerovores would be concentrated in the troposphere.
Traditional diamondoid nanomachinery designs [4] have employed 8 primary chemical elements, as detailed in Table 5 along with the associated atmospheric abundances [46] of each element. (Silicon is present in air as particulate dust which may be taken as ~28% Si for crustal rock [5], with a global average dust concentration of ~0.0025 mg/m³).

The requirement for elements that are relatively rare in the atmosphere greatly constrains the potential nanomass and growth rate of airborne replicators. However, note that at least one of the classical designs exceeds 91% CHON by weight. Although it would be very difficult, it is at least theoretically possible that replicators could be constructed almost solely of CHON, in which case such devices could replicate relatively rapidly using only atmospheric resources, powered by sunlight. A worldwide blanket of airborne replicating dust or “aerovores” that blots out all sunlight has been called the “gray dust” scenario [47]. (There have already been numerous experimental aerial releases of recombinant bacteria [48].)

Table 5. Element Usages by Weight in Classical Diamondoid Nanorobot Designs Compared to Atmospheric Element Abundances
Chemical Element	Fine Motion Controller	Neon Gas Pump	Differential Gear	Total Atmospheric Abundance
N	25.19%	3.56%	5.91%	7.81 × 10^-1
O	7.20%	6.66%	3.95%	2.1–2.4 × 10^-1
C	57.71%	24.84%	19.87%	9.87 × 10^-5
H	1.35%	2.05%	0.58%	1–300 × 10^-5
CHON	91.45%	37.11%	30.31%	>1 × 10^-5
Si	4.13%	52.20%	52.60%	~5 × 10^-10
S	3.65%	7.98%	7.66%	~5 × 10^-10
F	0.77%	0%	0%	~3 × 10^-14
P	0%	2.71%	9.43%	~1 × 10^-20
Total:	100.00%	100.00%	100.00%	1

Two independent constraints on gray dust replication speed are materials and energy availability, and both methods suggest that t ~ 10,000 sec for 1-micron replicators and ~1000 sec for 0.1-micron replicators. The analyses are as follows.

First, the mass current M_curr through the surface of a spherical nanorobot of radius R_nanois equal to the number of gas molecules/sec that collide with the fraction f ~ 10% of the nanorobot surface that consists of binding sites for those molecules, times the mass per gas molecule m_gas, divided by the number of collisions required for binding to occur, or N_encounter ~ 100 [6]; that is:

M_current = (4pR_nano²fc_gas / N_encounter) (2 kTm_gas / p)^½ (kg/sec)

(5)

where k = 1.381 × 10^-23 J/molecule-K (Boltzmann’s constant) and T ~ 300°K is ambient temperature in kelvins. The concentration of gas is c_gas = a_atmT_STPN_A / (V_molarT) (molecules/m³), where a_atm = atmospheric fractional abundance, T_STP = 273.15°K, N_A = 6.023 × 10²³ molecules/mole (Avogadro’s number), and molar volume at STP is V_molar = 22.4141 × 10^-3 m³/mole of an ideal gas.

The replication time t = M_nano / M_current, where M_nano = (4/3)pra_elementR_nano³, taking r ~ 2000 kg/m³ as nanorobot density and a_element as the fraction of nanorobot mass comprised of a given element. Hence:

t = [(N_encounterrV_molara_elemntR_nano) / (3 f a_atmT_STPN_A)] [(pT) / (2 km_gas)]^½ (sec)

(6)

Taking R_nano = 1 micron and allocating each a_element for the hypothetical CHON replicator as indicated in the second column of Table 6 gives the values of t shown at far right in Table 6.

The limiting elements are H and C, but C has the strongest impact on replication time, requiring a t ~ 12,300 sec. Since t scales as R_nano, reducing R_nano to 100 nm reduces t to ~1230 sec for this device. (Mechanical precompression and sortation [6] of gas molecules might reduce t by up to an order of magnitude but may impose partially offsetting internal volume utilization inefficiencies.).

Table 6. Replication Times of Airborne CHON Replicators as Restricted Solely by Chemical Element Abundances
Chemical Element	Used in Device a_element	Main Source Gas	Source Abundance a_atm	Source Molecule Mass m_gas (kg)	Replication Time (t)
N	28%	N₂	78.1%	4.6 × 10^-26	0.9 sec
O	8%	O₂	21.0%	5.3 × 10^-26	0.9 sec
C	62%	CO₂	0.0099%	7.3 × 10^-26	12,300 sec
H	2%	H₂O	0.001–0.3%	3.0 × 10^-26	20–6130 sec

Second, the solar energy flux into the nanorobot, assuming that a fraction f of its surface is photosensitive with energy conversion efficiency e, is P_nano = eI_solarf pR_nano². The energy required to build a nanorobot is E_nano ~ M_nano E_diss, hence the replication time is t = E_nano / P_nano, or:

t = (4 rE_dissR_nano) / (3 f eI_solar) (sec)

(7)

Taking r = 2000 kg/m³, E_diss ~ 100 MJ/kg, f = 50%, e = 10%, and I_solar = 100–400 W/m², then for R_nano = 1 micron, t ~ 11,000–53,000 sec; for R_nano = 100 nm, t = 1100–5300 sec.

Since replication of an airborne CHON replibot is primarily carbon-limited, in theory the entire global atmospheric carbon mass of ~5.2 × 10¹⁴ kg C is available for conversion into M_gd = 8.4 × 10¹⁴ kg of CHON nanomass, assuming a 62% carbon content by weight (Table 6).

However, because the machines are solar powered, the active population of gray dust nanorobots is restricted to one optical depth of such devices. To a very crude first approximation (e.g., ignoring contributions from scattered and reflected photons), one optical depth occurs when the cumulative cross-sectional area of the nanorobot population equals the surface area of Earth, so the maximum total mass of continuously active CHON airborne nanorobots is:

M_total ~ (16p / 3) r R_nanoR_Earth² (kg)	(8)
= 1.4 × 10¹² kg for R_nano = 1 micron
= 3.7 × 10¹¹ kg for R_nano = 275 nm
= 1.4 × 10¹¹ kg for R_nano = 100 nm

Once the expanding nanorobot population reaches one optical depth (requiring ~0.2% of all atmospheric carbon, or ~3 months of current anthropogenic airborne carbon releases), the replication rate of the gray dust ceases to grow exponentially and becomes essentially constant — a phenomenon which may be called the “opacity brake effect”. (One optical depth of uniformly distributed R_nano = 275 nm aerovores represents a particle number density of ~5 × 10⁸ m^-3.)

After the opacity brake point has been reached, a constant nanomass production rate of M_total/t ~ 1.4 × 10⁸ kg/sec ensues until exhaustion of the limiting atmospheric carbon resource. Current instrumentation can detect ~1% variations in the solar constant, so the limit for early bolometric detection is probably ~1% M_total, when ~0.002% of atmospheric carbon has been converted to nanomass.

Dust monitors in late 20th-century wafer-fab clean rooms regularly measure dust densities of ~10 particles/m³ at 0.5 microns and larger [49], potentially allowing detection as early as <10^-8 M_total if more highly discriminating monitors can be developed.

If the replibots settle out on the planetary surface and continue replicating there (Section 8.3), they could deprive the ecology of needed sunlight without darkening the sky, but their effects (e.g., a fine gray dust covering everything on the surface) would also be detectable far sooner than the 1% M_total point.

Since replication rate and opacity per unit nanomass vary inversely with R_nano, the most efficient gray dust replibot tasked with opacifying the atmosphere as quickly as possible will have the minimum possible size. (Replication time varies with thickness for a sheetlike nanorobot configuration.) The minimum replibot size is driven by UV radiation damage rates on nanomachinery [4].

Consider the smallest possible replicator with mass M_init = 1.7 × 10^-18 kg (Section 3.0); constructed as a spherical shape of density r = 2000 kg/m³, the radius of this core replicator is R_core ~ 59 nm. The core is surrounded by a radiation shield of thickness d and density ~r. The most dangerous is UV-B at l ~ 280 nm which will conservatively be taken as ~5 W/m² intensity near ground level [4], equivalent to D₀ = 7 × 10¹⁸ photons/m²-sec. The number of bonds cleaved inside the nanorobot is N_cleave = pR_nano²q_yt_lifeD₀exp(-4pk_xd / l), where q_y is quantum yield (bonds cleaved / photons absorbed), t_life is mean time to failure, and k_x is extinction coefficient.

k_x ~ 2.26 for graphite at 280 nm [50], a 2250 kg/m³ semimetal that is probably the most UV-absorptive CHON shield material. q_y = 10^-4 to 10^-1 for CHON polymers [51] and various proteins, viruses and phages [52]; following Drexler [4], we adopt q_y ~ 0.01 here (the exact choice is not critical to our conclusions). From Eqn. 7, t ~ c_tR_nano, where c_t ~ 10¹⁰ sec/m. Taking t_life = t n_t, where n_t is the number of offspring constructed before replibot failure, and assuming that N_cleave³ 1 implies device failure [4], then:

(R_core + d) £R_nano£ [N_cleave (exp(4pk_xd / l)) / (pq_yn_tc_tD₀)]^1/3

(9)

for replibots that produce n_t offspring before failing. The number of generations needed to replicate one optical depth of nanorobots worldwide, starting from a single device, is n_t = ln(M_total / M_init) = 65–60 for R_nano = 0.1–1 microns. Taking n_t ~ 64, Eqn. 9 defines the smallest gray dust replibot as R_nano ~275 nm (mass ~ 1.7 × 10^-16 kg) with a d ~ 215 nm thick graphite UV shield assuming N_cleave = 1.

The smallest replibot that can replicate only once before it fails (e.g., n_t = 1) has R_nano ~ 230 nm with a d ~ 170 nm shield taking N_cleave= 1, or R_nano ~ 175 nm with a d ~ 115 nm shield taking N_cleave = 100 for more robust devices.

From Eqns. 1 and 8, and neglecting dispersal velocity limitations (Section 4.0) the minimum possible time to reach some fraction f_opac of global atmospheric opacity is:

t_opac = t ln(4 f_opacR_Earth² / R_nano²) (sec)

(10)

For airborne CHON replibots with R_nano = 275 nm and t ~ 2750 sec, 1% of opacity is reached in t_opac ~ 1.85 days, 100% opacity in 2.0 days, leaving a response time of ~3.5 hours between first detection at 1% opacity and complete opacity at 100%. If uniformly distributed throughout the atmosphere, the dust density at 100% opacity would amount to ~0.085 mg/m³ for 275-nm nanorobots, about equal to the typical ~0.05 mg/m³ dust density normally found in the air of most industrialized Western cities [69].

After 100% opacity is reached, another t_end = t (M_gd–M_total) / M_total = 72 days would be required to convert the remaining atmospheric carbon resource into nanomass. However, post-opacity the gray dust replication rate is no longer exponentiating so the defensive nanorobots can quickly catch up.

The most efficient cleanup strategy appears to be the use of air-dropped non-self-replicating nanorobots equipped with prehensile microdragnets. Consider a planetwide dragnet comprised of a square mesh of fibers, with mesh aperture size l_mesh, mesh fibers of thickness d_fiber, and total dragnet area A_net covering Earth’s entire surface area A_Earth = 4pR_Earth² = A_net.

Minimum fiber thickness is d_fiber ≥ (p_airl_mesh² / 4 s_fiber)^½, where p_air ≤ 2 atm is the maximum air pressure resisting movement of the net through the air and fiber failure strength is very conservatively taken as s_fiber ~ 10¹⁰ N/m² for carbon nanotubes. For l_mesh≤ 460 nm (smallest possible gray dust replibot, see above), d_fiber ≥ 1 nm. Simple geometry gives the total volume of required square-grid dragnet as:

V_dragnet ~ 2 d_fiber² [(A_net^½) + (A_net / l_mesh)] (m³)

(11)

Taking A_net = A_Earth = 5.10 × 10¹⁴ m², l_mesh = 460 nm and d_fiber = 1 nm, then V_dragnet = 2200 m³. This dragnet may be carried aloft by a fleet of N_bot = V_dragnet / f_vV_bot spherical defensive nanorobots, each of which uses some fraction f_v of its internal storage volume to hold a piece of the dragnet, where individual defensive nanorobot volume is V_bot = (4/3)p R_nano³.

Taking f_v = 5% and R_nano = 0.62 micron, V_bot = 1 micron³ and N_bot = 4.4 × 10²² defensive nanorobots of total mass ~V_botrN_bot = 8.8 × 10⁷ kg (of which ~4.4 × 10⁶ kg is dragnet). Thus a single 88-kg payload of non-self-replicating defensive nanorobots launched from each of 10⁶ deployment sites worldwide (mean site separation ~23 km, ~one per town) to an altitude just above the gray dust replibots can deploy an Earth-covering net, which then descends through the air, selectively filtering out the gray dust replibots.

The time required for this dragnet to sweep the entire atmospheric volume of Earth once is t_sweep ~ V_air / (4pR_Earth²v_nano) ~ 24 hours, taking nanorobot aeromotive velocity v_nano ~ 0.1 m/sec for power densities appropriate to solar powered nanodevices [6] and V_air ~ 4.36 × 10¹⁸ m³ at ~1 atm pressure and room temperature.

Possible false targets that may be encountered during the sweep include airborne fungal spores at 10–500 m^-3 indoors and 100–1000 m^-3 outdoors [53]; bacteria at 0–500 m^-3 indoors, 179–1083 m^-3 outdoors [53], and ~140 m^-3 up to ~3 km altitude [38]; and inert dust particles of various sizes peaking in number density near ~20 nm [46], in concentrations ranging from 10 m^-3 in semiconductor fab plant clean rooms up to 2 × 10⁷ m^-3 in quiet country air, 6 × 10⁷ m^-3 over residential city air, 1.5 × 10⁸ m^-3 in the worst congested downtown city air, and >2.7 × 10⁸ m^-3 in rooms with smokers present [49, 54].

Of course, multiple cleansing sweeps may be required, insect^a and bird^b management and biocompatibility protocols must be devised, exterior surfaces must be appropriately hydrophobic to avoid providing condensation nuclei for cloud and fog formation, and so forth.

The total machine volume of one optical depth of 275-nm gray dust replibots is 1.9 × 10⁸ m³, making an average cleanup requirement of only ~4500 micron³ of targets per defensive nanorobot. A spherical knapsack comprised of additional mesh material having an enclosed volume of 4500 micron³ adds only 11% to the onboard mesh storage requirement.

Each defensive nanorobot deploys a (110 micron)² ~ 12,100 micron² section of the planetwide dragnet. In theory, if this section were curved into a huge spherical knapsack, it would make a storage volume of 125,000 micron³ — enough to hold the equivalent of ~28 optical depths of gray dust replibots during passage through locally dense clouds of target airborne nanoreplicators.

Each defensive nanorobot requires ~66 nN of motive force and ~6600 pW of onboard power to overcome drag loss [6] on the ~5.3 cm length of dragnet fiber that it is passing through the air at 0.1 m/sec. This power is provided by a rear-deployed, 30% efficient, 55 micron², ~10 nm thick solar collector film that stows in a 0.55 micron³ volume before deployment and adds only ~45 pW to drag power after deployment.

When fully deployed, the defensive fleet contributes <0.5% additional atmospheric opacity, and clears air for an energy cost of ~5.8 J/m³ of contaminated atmosphere, per pass. Defensive nanorobot locomotion in the viscous flight regime may be provided by screw drives, viscous anchoring via the prehensile dragnet, or other means [6].

The Stokes settling velocity [6] in air is ~240 micron/sec for R_nano = 1 micron, ~20 micron/sec for R_nano = 275 nm and ~5 micron/sec for R_nano = 100 nm, giving 10-km passive fall times (in still atmosphere) of 1.3 years, 16 years and 67 years, respectively.

Alternative airborne or ground-based atmospheric filtration configurations that could permit more rapid filtering are readily envisioned. For example, since drag power varies as the square of the velocity, then by increasing mesh volume 10,000-fold while decreasing airflow velocity 100-fold, total drag power remains unchanged but whole-atmosphere turnover proceeds 100-fold faster, e.g., ~15 minutes.

^a There are ~10¹⁸–10¹⁹ insects on Earth [75–77]. The average insect devotes ~35% of body volume to its respiratory system [78], which is mostly gas-phase diffusional but with some very primitive active ventilation. If average insect volume is ~0.6 mm³ [77], then the worldwide insect population has ~2 × 10⁹ m³ of tracheal air volume which could accumulate ~10¹⁶ aerovores if insects are exposed to replibot-contaminated air at a concentration equivalent to ~1% atmospheric opacity.

In this case ~10^-9 of the global aerovore population resides inside insects (~1 replibot per 1000 insects at 1% opacity), requiring careful quarantine or inspection and release protocols for insects passing through the dragnet.

^b There are ~300 billion birds on Earth [70]. The average bird devotes 20% of body volume to its respiratory system [71], mostly unidirectional airflow unlikely to permanently trap gray dust, but ~20% of the bird respiratory volume consists of tidally exchanged air in 8–9 anterior and posterior air sacs, and air spaces in the bones [71].

Assuming dead air in birds represents 38% of tidal volume as in humans [6], and that the average bird is ~500 cm³ in volume, then the worldwide bird population has ~2 × 10⁶ m³ of respiratory dead air which could accumulate ~10¹³ aerovores if the birds are breathing replibot-contaminated air at a concentration equivalent to ~1% atmospheric opacity.

In this case ~10^-12 of the global aerovore population resides inside bird respiratory systems (~40 replibots per bird at 1% opacity), necessitating specialized quarantine or inspection and release protocols for birds passing through the dragnet. Under similar exposure, ~7 × 10¹³ aerovores (~3 × 10^-12 of the total) could reside in all human lungs worldwide, or ~10,000 aerovores/person.

8.3 Gray Lichens

Gray lichens consuming the Earth would be hindered by lack of energy resources and high temperatures as they approached the Earth’s core.
Colonies of symbiotic algae and fungi known as lichens (which some have called a form of sub-aerial biofilm) are among the first plants to grow on bare stone, helping in soil formation by slowly etching the rock [55]. Lithobiontic microbial communities such as crustose saxicolous lichens penetrate mineral surfaces up to depths of 1 cm using a complex dissolution, selective transport, and recrystallization process sometimes termed “biological weathering” [56].

Colonies of epilithic (living on rock surfaces) microscopic bacteria produce a 10 micron thick patina on desert rocks (called “desert varnish” [57]) consisting of trace amounts of Mn and Fe oxides that help to provide protection from heat and UV radiation [57–59]. In theory, replicating nanorobots could be made almost entirely of nondiamondoid materials including noncarbon chemical elements found in great abundance in rock such as silicon, aluminum, iron, titanium, and oxygen (Section 2). The subsequent ecophagic destruction of land-based biology by a maliciously programmed noncarbon epilithic replicator population that has grown into a significant nanomass is the “gray lichen” scenario.

The growth rate of gray lichens on the surface of the Earth will be primarily energy-limited, not materials-limited.

While it is true that chemolithotrophic microorganisms such as Thiobacillus ferrooxidans use reduced iron and sulfur compounds for their energy source [60–62], and that other chemolithotrophic bacteria can metabolize inorganic carbon (e.g., assimilating CO₂ from carbonate rock) using a pathway similar to green plants [63], such energy sources appear to be far less plentiful than ambient sunlight because most rocks are already fully oxidized. (For example, the oxidation of Fe⁺⁺ to Fe⁺⁺⁺ by chemolithotrophs liberates only 0.75 MJ/kg [64], as compared to ~16 MJ/kg for the combustion of glucose in oxygen [6].)

Assuming that up to 400 W/m² in the visible spectrum is harvested with 30% efficiency for 8 hours/day over the entire landmass of Earth, the 6 × 10¹⁵ watts theoretically available could produce at most ~6 × 10⁷ kg/sec of mineral nanomass taking E_diss ~ 100 MJ/kg as before. Even assuming an optimal dispersal pattern, ~2.6 years would be required for the growing mineral nanomass to equal the terrestrial biomass (~5 × 10¹⁵ kg; Section 3), whereupon the top ~1 cm of Earth’s entire continental land area would have been converted to nanomass.

Continuous direct census sampling of the Earth’s land surfaces will almost certainly allow early detection, since mineralogical nanorobots should be easily distinguishable from inert rock particles and from organic microbes in the top 3–8 cm of soil, typically 2.1 × 10¹³ m^-3 of aerobic bacteria, 5.6 × 10¹² m^-3 of actinomycetes, 5.2 × 10¹² m^-3 of anaerobic bacteria, 3.2 × 10¹¹ m^-3 fungi, and 6.7 × 10¹⁰ m^-3 of algae [64].

8.4 Malicious Ecophagy

A successful ecophagic attack would leave a dead planet.
More difficult scenarios involve ecophagic attacks that are launched not to convert biomass to nanomass, but rather primarily to destroy biomass. The optimal malicious ecophagic attack strategy appears to involve a two-phase process.

In the first phase, initial seed replibots are widely distributed in the vicinity of the target biomass, replicating with maximum stealth up to some critical population size by consuming local environmental substrate to build nanomass.

In the second phase, the now-large replibot population ceases replication and exclusively undertakes its primary destructive purpose. More generally, this strategy may be described as Build/Destroy.

During the Build phase of the malicious “badbots”, and assuming technological equivalence, defensive “goodbots” enjoy at least three important tactical advantages over their adversaries:

Preparation — defensive agencies can manufacture and position in advance overwhelming quantities of (ideally, non-self-replicating) defensive instrumentalities, e.g., goodbots, which can immediately be deployed at the first sign of trouble, with minimal additional risk to the environment,
Efficiency — while badbots must simultaneously replicate and defend themselves against attack (either actively or by maintaining stealth), goodbots may concentrate exclusively on attacking badbots (e.g., because of their large numerical superiority in an early deployment) and thus enjoy lower operational overhead and higher efficiency in achieving their purpose, all else equal; and
Leverage — in terms of materials, energy, time and sophistication, fewer resources are generally required to confine, disable, or destroy a complex machine than are required to build or replicate the same complex machine from scratch (e.g., one small bomb can destroy a large bomb-making factory; one small missile can sink a large ship).

However, once the badbots enter their Destroy phase, only the first advantage of the defenders (i.e., preparation) remains fully effective. Of course, a total mass M_goodbots of nonreplicating defensive nanorobots can hold constant a population M_badbots of self-replicating biovorous nanorobots if M_goodbots ≥ (t_destroy / t) M_badbots, where t_destroy is the time required for a goodbot to find and permanently restrain, disable or destroy a badbot (which has a replication time t); usually, t_destroy < t.

Nevertheless it is most advantageous to engage a malicious ecophagic threat while it is still in its Build phase. This requires foresight and a commitment to extensive surveillance by the defensive authorities. A complete analysis is beyond the scope of this paper, but two simple examples will suffice to illustrate the level of surveillance required.

First, consider a population of N_bot replibots that have infested a human body and are about to enter their Destroy phase. These badbots are assumed to be motile spherical nanorobots of radius R_nano, capable of drilling through tissue at velocity v_nano; encountered tissue is destroyed with efficiency k_e, and a mass fraction f_dest of the biomass must be destroyed to produce death. The time required to kill is:

t_kill = f_destM_body / (k_epr_bodyR_nano²v_nanoN_bot)

(12)

where M_body is body mass and r_body is mean body density. Power is provided by combustion at conversion efficiency e of onboard H₂/O₂ fuel (energy density E_fuel ~ 4.5 × 10¹⁰ J/m³ [6]) compressed to 10,000 atm, stored in tanks representing some fraction f_fuel of nanorobot volume.

The power produced is P_nano = (4 p / 3) R_nano³f_fuelE_fuele / t_kill, exhausting the stored fuel after t_kill. Setting this available power P_nano equal to Stokes drag power P_drag = 6 p hR_nanov_nano² and substituting for t_kill gives maximum drilling velocity:

v_nano ≤ (2 p k_er_bodyf_fuelE_fueleN_botR_nano⁴) / (9 hf_destM_body)

(13)

where h is mean tissue viscosity. The mass fraction of badbots that can produce death in a time t_kill is f_n = M_badbot / M_body, where total badbot mass is M_badbot = (4/3) p r_nanoR_nano³N_bot and r_nano is nanorobot density. Obtaining N_bot by solving Eqn. 13 for N_bot, then substituting v_nano obtained from Eqn. 12, gives:

f_n = [(4 f_destr_nano) / (k_e r_body)] [h / (2 f_fuelE_fuelet_kill)]^½

(14)

The number of attacking badbots is then:

N_bot = 3 f_nM_body / (4 pr_nanoR_nano³)

(15)

Taking f_dest = 0.1 (10%), k_e = 0.5 (50%), e = 0.5 (50%), f_fuel = 0.1 (10%), R_nano = 1 micron, r_nano = 2000 kg/m³, h ~ 1000 kg/m-sec [6], and r_body = M_body / V_body where M_body = 70 kg and body volume V_body = 0.06 m³ [6], then a kill time t_kill = 1 sec requires f_n = 6 × 10^-4 and N_bot = 5 × 10¹² badbots. However, if the body is monitored continuously such that a whole-body badbot dose as small as 1 mg can be detected, then f_n ~ 10^-8 (N_bot ~ 10⁸ badbots) and t_kill increases dramatically to ~60 years, giving plenty of time for defense.

If the potential victim’s body (comprised of N_cell ~10¹⁴ native and foreign cells [6]) contains a continuously-circulating population N_botM of cell-monitoring nanorobots each requiring c_time ~ 100 sec/cell to enter and examine a cell for badbot intruders, and if every cell in the body is to be checked once every day (t_body ~ 10⁵ sec), then N_botM = c_time N_cell / t_body ~ 10¹¹ cell-monitors, with total fleet volume ~ 0.1 cm³ assuming R_nano = 1 micron. At f_n ~ 10^-8, a badbot resides, on average, in one of every 10⁶ cells, assuming uniform distribution. The hypothesized monitoring system examines ~10⁶ cells every 0.001 sec, so a badbot infection of this magnitude is first detected in ~1 millisec, allowing a massive and immediate “immune” response.

Second, consider the defense of the entire eukaryotic biosphere. Excluding bacteria assumed to represent about half of global biomass and assuming an average eukaryotic cell size of 20 microns, there are ~3 × 10²⁶ eukaryotic cells on Earth.

If each cell is visited and examined, on average, about once a year with time spent per cell c_time = 100 sec/cell as before, this implies a global examination rate of X_cell ~ 10¹⁹ cells/sec and a requirement for X_cellc_time ~ 10²¹ cell-monitoring nanorobots, representing a total worldwide nanomachine volume of ~1000 m³ of 1-micron nanorobots consuming ~10 GW (~0.1% total current human global power generation) assuming ~10 pW/device.

In this surveillance regime, a ~1 mg infestation of 1-micron badbots in a 3 meter wide, 30 meter tall redwood tree (f_n ~ 10^-11) is first detected in ~100 millisec — again, triggering a prompt corrective response.

9.0 Conclusions

The smallest plausible biovorous nanoreplicator has a molecular weight of ~1 gigadalton and a minimum replication time of perhaps ~100 seconds, in theory permitting global ecophagy to be completed in as few as ~10⁴ seconds. However, such rapid replication creates an immediately detectable thermal signature enabling effective defensive policing instrumentalities to be promptly deployed before significant damage to the ecology can occur.

Such defensive instrumentalities will generate their own thermal pollution during defensive operations. This should not significantly limit the defense strategy because knapsacking, disabling or destroying a working nanoreplicator should consume far less energy than is consumed by a nanoreplicator during a single replication cycle, hence such defensive operations are effectively endothermic.

Ecophagy that proceeds near the current threshold for immediate climatological detection, adding perhaps ~4°C to global warming, may require ~20 months to run to completion, which is plenty of advance warning to mount an effective defense.

Ecophagy that progresses slowly enough to evade easy detection by thermal monitoring alone would require many years to run to completion, could still be detected by direct in situ surveillance, and may be at least partially offset by increased biomass growth rates due to natural homeostatic compensation mechanisms inherent in the terrestrial ecology.

Ecophagy accomplished indirectly by a replibot population pre-grown on nonbiological substrate may be avoided by diligent thermal monitoring and direct census sampling of relevant terrestrial niches to search for growing, possibly dangerous, pre-ecophagous nanorobot populations.

Specific public policy recommendations suggested by the results of the present analysis include:

an immediate international moratorium on all artificial life experiments implemented as nonbiological hardware. In this context, “artificial life” is defined as autonomous foraging replicators, excluding purely biological implementations (already covered by NIH guidelines [65] tacitly accepted worldwide) and also excluding software simulations which are essential preparatory work and should continue. Alternative “inherently safe” replication strategies such as the broadcast architecture [66] are already well-known.
continuous comprehensive infrared surveillance of Earth’s surface by geostationary satellites, both to monitor the current biomass inventory and to detect (and then investigate) any rapidly-developing artificial hotspots. This could be an extension of current or proposed Earth-monitoring systems (e.g., NASA’s Earth Observing System [67] and disease remote-sensing programs [93]) originally intended to understand and predict global warming, changes in land use, and so forth — initially using non-nanoscale technologies. Other methods of detection are feasible and further research is required to identify and properly evaluate the full range of alternatives.
initiating a long-term research program designed to acquire the knowledge and capability needed to counteract ecophagic replicators, including scenario-building and threat analysis with numerical simulations, measure/countermeasure analysis, theory and design of global monitoring systems capable of fast detection and response, IFF (Identification Friend or Foe) discrimination protocols, and eventually the design of relevant nanorobotic systemic defensive capabilities and infrastructure.

A related long-term recommendation is to initiate a global system of comprehensive in situ ecosphere surveillance, potentially including possible nanorobot activity signatures (e.g. changes in greenhouse gas concentrations), multispectral surface imaging to detect disguised signatures, and direct local nanorobot census sampling on land, sea, and air, as warranted by the pace of development of new MNT capabilities.

10.0 Acknowledgements

The author thanks Robert J. Bradbury, J. Storrs Hall, James Logajan, Markus Krummenacker, Thomas McKendree, Ralph C. Merkle, Christopher J. Phoenix, Tihamer Toth-Fejel, James R. Von Ehr II, and Eliezer S. Yudkowsky for helpful comments on earlier versions of this manuscript; J. S. Hall for the word “aerovore”; and R. J. Bradbury for preparing the hypertext version of this document.

11.0 References

1: Bill Joy, Why the future doesn’t need us, Wired (April 2000); response by Ralph Merkle, Text of prepared comments by Ralph C. Merkle at the April 1, 2000 Stanford Symposium organized by Douglas Hofstadter.
2: K. Eric Drexler, Engines of Creation: The Coming Era of Nanotechnology, Anchor Press/Doubleday, New York, 1986.
3: Joshua Lederberg, “Infectious History”, Science 288 (14 April 2000):287–293.
4: K. Eric Drexler, Nanosystems: Molecular Machinery, Manufacturing, and Computation, John Wiley & Sons, NY, 1992.
5: Robert C. Weast, Handbook of Chemistry and Physics, 49th Edition, CRC, Cleveland OH, 1968.
6: Robert A. Freitas Jr., Nanomedicine, Volume I, Landes Bioscience, Georgetown, TX, 1999.
7: Edward L. Alpen, Radiation Biophysics, Second Edition, Academic Press, New York, 1998.
8: Walter M. Elsasser, “Earth”, Encyclopedia Britannica 7 (1963):845–852.
9: G. Buntebarth, A. Gliko, “Heat Flow in the Earth’s Crust and Mantle” in A.S. Marfunin, ed., Advanced Mineralogy, Volume 1: Composition, Structure, and Properties of Mineral Matter: Concepts, Results, and Problems, Springer-Verlag, New York, 1994, pp. 430–435.
10: Karsten Pedersen, “The deep subterranean biosphere”, Earth Sci. Rev. 34 (1993):243–260.
11: Todd O. Stevens, James P. McKinley, Lithoautotrophic Microbial Ecosystems in Deep Basalt Aquifers, Science 270 (20 October 1995):450–454; see also: G. Jeffrey Taylor, Life Underground, PSR Discoveries, 21 December 1996.
12: Stephen Jay Gould, Life’s Grandeur: The Spread of Excellence from Plato to Darwin, Jonathan Cape, 1996.
13: Bill Cabage, Digging Deeply, September 1996.
14: James K. Fredrickson, Tullis C. Onstott, Microbes Deep Inside the Earth, Sci. Am. 275 (October 1996):68–73.
15: Richard Monastersky, Deep Dwellers: Microbes Thrive Far Below Ground, Science News 151 (29 March 1997):192–193.
16: Thomas Gold, The Deep Hot Biosphere, Copernicus Books, 1999; The deep, hot biosphere, Proc. Natl. Acad. Sci. 89(1992):6045–6049. See also: P.N. Kropotkin, “Degassing of the Earth and the Origin of Hydrocarbons”, Intl. Geol. Rev. 27 (1985):1261–1275.
17: Karl Leif Bates, Michigan’s natural gas fields: Blame it on underground bacteria, The Detroit News, 12 September 1996.
18: JoAnn Gutin, Making bacteria move, Princeton Weekly Bulletin, 17 November 1997.
19: Robert A. Freitas Jr., William P. Gilbreath, eds., Advanced Automation for Space Missions, Proceedings of the 1980 NASA/ASEE Summer Study held at the University of Santa Clara, Santa Clara, CA, June 23-August 29, 1980; NASA Conference Publication CP-2255, November 1982.
20: R.K. Dixon, S. Brown, R.A. Houghton, A.M. Solomon, M.C. Trexler, J. Wisniewski, Carbon Pools and Flux of Global Forest Ecosystems, Science 263 (14 January 1994):185–190.
21: Christopher B. Field, Michael J. Behrenfeld, James T. Randerson, Paul Falkowski, Primary Production of the Biosphere: Integrating Terrestrial and Oceanic Components, Science 281 (10 July 1998):237–240.
22: Peter M. Vitousek, Harold A. Mooney, Jane Lubchenco, Jerry M. Melillo, Human Domination of Earth’s Ecosystems, Science 277 (25 July 1997):494–499.
23: Colin J. Campbell, Jean H. Laherrere, The End of Cheap Oil, Scientific American 278(March 1998):78–83; Robert G. Riley Enterprises, World Petroleum Reserves, 1999; L.F. Ivanhoe, Future world oil supplies: There is a finite limit, World Oil, October 1995.
24: James P. Kennett, Kevin G. Cannariato, Ingrid L. Hendy, Richard J. Behl, Carbon Isotopic Evidence for Methane Hydrate Instability During Quaternary Interstadials, Science 288 (7 April 2000):128–133.
25: World Coal Institute, Coal — Power for Progress, Third Edition, January 1999; Statistics Canada, World Coal Reserves, 1996; U.S. Coal Reserves: 1997 Update, February 1999, Energy Information Administration, Washington, DC.
26: F.J. Millero, Thermodynamics of the carbon dioxide system in the oceans, Geochim. Cosmochim. Acta 59 (1995):661–677; see also F.J. Millero, “Carbon Dioxide in the South Pacific”.
27: Michael T. Madigan, John M. Martinko, Jack Parker, eds., Brock’s Biology of Microorganisms, 9th Edition, Prentice-Hall, NJ, 1999; Kenneth J. Ryan, ed., Sherris Medical Microbiology: An Introduction to Infectious Diseases, 3rd Edition, McGraw-Hill, New York, 1994.
28: ORNL, Major World Ecosystem Complexes Ranked by Carbon in Live Vegetation, April 1997.
29: J.H. Martin, The IronEx Group, Testing the iron hypothesis in the ecosystems of the equatorial Pacific Ocean, Nature 371 (1994):123–129; Sallie W. Chisholm, The iron hypothesis: Basic research meets environmental policy, Rev. Geophys. 33 (1995):Supplement. See also Extra iron makes blue deserts bloom, New Scientist 152 (12 October 1996).
30: Richard W. Hughes, Ruby & Sapphire, RWH Publishing, Boulder CO, 1997.
31: F. Albert Cotton, Geoffrey Wilkinson, Advanced Inorganic Chemistry: A Comprehensive Text, Second Edition, John Wiley & Sons, New York, 1966.
32: Ralph C. Merkle, personal communication, 22 March 2000.
33: P.G. Jarvis, Tree Physiol. 2 (1986):347-.
34: Oliver L. Phillips et al, Changes in the Carbon Balance of Tropical Forests: Evidence from Long-Term Plots, Science 282 (16 October 1998):439–442.
35: S. Fan, M. Gloor, J. Mahlman, S. Pacala, J. Sarmiento, T. Takahashi, P. Tans, A Large Terrestrial Carbon Sink in North America Implied by Atmospheric and Oceanic Carbon Dioxide Data and Models, Science 282 (16 October 1998):442–446.
36: D. Stramski, D.A. Kiefer, Light Scattering by Microorganisms in the Open Ocean, Prog. Oceanogr. 28 (1991):343.
37: Curtis D. Mobley, “Chapter 43. The Optical Properties of Water”, in Michael Bass, ed., Handbook of Optics, Volume I, McGraw-Hill, Inc., New York, 1995, pp. 43.3–43.56.
38: Neil A. Campbell, Jane B. Reece, Lawrence G. Mitchell, Biology — Interactive Study Guide, Benjamin/Cummings Science, San Francisco, CA, 1999. See also: Paul Broady, BIOL 113 — Diversity of Life, lecture notes.
39: William B. Whitman, David C. Coleman, Prokaryotes: the unseen majority, Proc. Natl. Acad. Sci. (USA) 94 (June 1998):6578–6583.
40: B.R. Strain, J.D. Cure, eds., Direct Effects of Increasing Carbon Dioxide on Vegetation, Publ. ER-0238, U.S. Department of Energy, Washington, DC, 1985; R.J. Luxmoore, R.J. Norby, E.G. O’Neill, in Forest Plants and Forest Protection, 18th Intl. Union of Forestry Research Organizations (IUFRO), World Congress, Div. 2, 1987, IUFRO Secretariate, Vienna, 1987, Vol. 1, pp. 178–183; P.S. Curtis, B.G. Drake, P.W. Leadley, W.J. Arp, D.F. Whigham, Oecologia 78 (1989):20; D. Eamus, P.G. Jarvis, Adv. Ecol. Res. 19 (1989):1; P.G. Jarvis, Philos. Trans. R. Soc. London B 324 (1989):369; R.J. Norby, E.G. O’Neill, New Phytol. 117 (1991):515.
41: Christian Korner, John A. Arnone III, Responses to Elevated Carbon Dioxide in Artificial Tropical Ecosystems, Science 257 (18 September 1992):1672–1675.
42: Eric T. Sundquist, The Global Carbon Dioxide Budget, Science 259 (12 February 1993):934–941.
43: Hubertus Fischer, Martin Wahlen, Jesse Smith, Derek Mastroianni, Druce Deck, Ice Core Records of Atmospheric CO₂ Around the Last Three Glacial Terminations, Science 283 (12 March 1999):1712–1714.
44: Peter G. Brewer, Gernot Friederich, Edward T. Peltzer, Franklin M. Orr Jr., Direct Experiments on the Ocean Disposal of Fossil Fuel CO₂, Science 284 (7 May 1999):943–945; Ocean studied for carbon dioxide storage, 10 May 1999.
45: C.N. Murray, L. Visintini, G. Bidoglio, B. Henry, Permanent Storage of Carbon Dioxide in the Marine Environment: The Solid CO₂ Penetrator, Energy Convers. Mgmt. 37 (1996):1067–1072.
46: Dennis K. Killinger, James H. Churnside, Laurence S. Rothman, “Chapter 14. Atmospheric Optics”, in Michael Bass, Eric W. Van Stryland, David R. Williams, William L. Wolfe, eds., Handbook of Optics, Volume I: Fundamentals, Techniques, and Design, Second Edition, McGraw-Hill, Inc., New York, 1995, pp. 44.1–44.50.
47: Ralph C. Merkle, personal communication, 6 April 2000.
48: Guy R. Knudsen, Louise-Marie C. Dandurand, Model for Dispersal and Epiphytic Survival of Bacteria Applied to Crop Foliage, paper presented at the 7th Symposium on Environmental Releases of Biotechnology Products: Risk Assessment Methods and Research Progress, 6–8 June 1995, Pensacola, FL.
49: Jake Page, Making the Chips that Run the World, Smithsonian 30 (January 2000):36–46.
50: A. Borghesi, G. Guizzetti, “Graphite (C)” in Edward D. Palik, ed., Handbook of Optical Constants of Solids II, Academic Press, New York, 1991, pp. 449–460.
51: B. Ranby, J.F. Rabek, Photodegradation, Photo-oxidation and Photostabilization of Polymers, John Wiley & Sons, New York, 1975.
52: William S. Spector, ed., Handbook of Biological Data, W.B. Saunders Company, Philadelphia PA, 1956.
53: W.J. Kowalski, William Bahnfleth, Airborne Respiratory Diseases and Mechanical Systems for Control of Microbes, HPAC (July 1998).
54: M. Edmund Speare, Wayne Anthony McCurdy, Allan Grierson, “Coal and Coal Mining”, Encyclopedia Britannica 5 (1963):961–975; Helmut E. Landsberg, “Dust”, Encyclopedia Britannica 7 (1963):787–791; and Gerrit Willem Hendrik Schepers, “Pneumonoconiosis”, Encyclopedia Britannica 18 (1963):99–100.
55: T.H. Nash, Lichen Biology, Cambridge University Press, Cambridge, 1996.
56: W.W. Barker, J.F. Banfield, “Biologically- versus inorganically-mediated weathering: relationships between minerals and extracellular polysaccharides in lithobiontic communities”, Chemical Geology 132 (1996):55–69; J.F. Banfield, W.W. Barker, S.A. Welch, A. Taunton, Biological impact on mineral dissolution: Application of the lichen model to understanding mineral weathering in the rhizosphere, Proc. Nat. Acad. Sci. (USA) 96 (1999):3404–3411. See also: W.W. Barker, “Interactions between silicate minerals and lithobiontic microbial communities (lichens)”.
57: Ronald L. Dorn, Theodore M. Oberlander, Microbial Origin of Desert Varnish, Science 213 (1981):1245–1247; R.L. Dorn, Rock varnish, Amer. Sci. 79 (1991):542–553.
58: W.W. Barker, S.A. Welch, S. Chu, J.F. Banfield, Experimental observations of the effects of bacteria on aluminosilicate weathering, Amer. Mineral. 83 (1998):1551–1563.
59: S.A. Welch, W.W. Barker, J.F. Banfield, Microbial extracellular polysaccharides and plagioclase dissolution, Geochim. Cosmochim. Acta 63 (1999):1405–1419.
60: K.L. Temple, A.R. Colmer, The autotrophic oxidation of iron by a new bacterium, Thiobacillus ferrooxidans, J. Bacteriol. 62 (1951):605–611.
61: P.A. Trudinger, “Microbes, Metals, and Minerals”, Minerals Sci. Eng. 3 (1971):13–25; C.L. Brierley, “Bacterial Leaching”, CRC Crit. Rev. Microbiol. 6 (1978):207–262; Microbiological mining, Sci. Am. 247 (February 1982):44–53.
62: A. Okereke, S.E. Stevens, Kinetics of iron oxidation by Thiobacillus ferrooxidans, Appl. Environ. Microbiol. 57 (1991):1052–1056.
63: Verena Peters, Peter H. Janssen, Ralf Conrad, Transient Production of Formate During Chemolithotrophic Growth of Anaerobic Microorganisms on Hydrogen, Curr. Microbiol. 38 (1999):285–289.
64: Mark S. Coyne, “Lecture 24 — Biogeochemical Cycling: Soil Mineral Transformations of Metals”, Agripedia: Introductory Soil Biology; “Lecture 3 — Soil as a Microbial Habitat: Microbial Distribution”, Agripedia: Introductory Soil Biology.
65: NIH Guidelines for Research Involving Recombinant DNA Molecules, January 1996 revision.
66: Ralph C. Merkle, Self-replicating systems and low cost manufacturing in M.E. Welland, J.K. Gimzewski, eds., The Ultimate Limits of Fabrication and Measurement, Kluwer, Dordrecht, 1994, pp. 25–32.
67: Links to Earth Observing System (EOS) Data and Information.
68: Paul E. Tiegs, Design and Operating Factors Which Affect Emissions from Residential Wood-Fired Heaters: Review and Update, 22 June 1995; Stephen Black, A.B. Donaldson, “Some Observations on Operation of a Diesel Engine With Ethanol and Ethanol-Water Blends and Combustion Air Preheat”, Spring 1998; A. Ngaloken Gintings et al, “The relationship between waste wood management and the risk of transboundary haze from forest fire”, 17 December 1998.
69: World Resources Institute, World Resources 1988–89, Basic Books, Inc., New York, 1988, p. 169; EPA, Federal Register 61 (13 December 1996):657–63.
70: Sankar Chatterjee, The Rise of Birds: 225 Million Years of Evolution, Johns Hopkins University Press, Baltimore, MD, 1997.
71: Paul R. Ehrlich, David S. Dobkin, Darryl Wheye, Adaptations for Flight, 1988.
72: H. J. Morowitz, M. E. Tourtellotte, The Smallest Living Cells, Sci. Am. 206 (March 1962):117–126; H.J. Morowitz, Prog. Theoret. Biol. 1 (1967):1.
73: A. R. Mushegian, E. V. Koonin, A minimal gene set for cellular life derived by comparison of complete bacterial genomes, Proc. Natl. Acad. Sci. (USA) 93 (17 September 1996):10268–10273.
74: R. Himmelreich, H. Hilbert, H. Plagens, E. Pirkl, B.C. Li, R. Herrmann, Complete sequence analysis of the genome of the bacterium Mycoplasma pneumoniae, Nucleic Acids Res. 24 (15 November 1996):4420–4449.
75: C. B. Williams, Patterns in the Balance of Nature and Related Problems in Quantitative Ecology, Academic Press, London, 1964.
76: C. W. Sabrosky, “How many insects are there?” in Insects, The Yearbook of Agriculture, U.S. Department of Agriculture, Washington, DC, 1952.
77: Numbers of Insects (Species and Individuals), Department of Entomology, National Museum of Natural History.
78: Nelson Thompson, “Biology/Entomology 173. Insect Physiology, Spring 1998, Lecture 17: Respiration”, 6 November 1997; Some biological problems involving diffusion.
79: J. Storrs Hall, personal communication, 6 May 2000.
80: U.S. Bureau of the Census, Statistical Abstract of the United States: 1996, 116th Edition, Washington, DC, October 1996.
81: “…there are dozens of HIV-like viruses in wild monkey populations, and if natural transfer of AIDS viruses from chimpanzees to monkeys has already occurred, there is no reason why it should not happen again.” Beatrice Hahn, Howard Hughes Medical Institute scientist, quoted in: Declan Butler, Analysis of polio vaccine could end dispute over how AIDS originated, Nature 404 (2 March 2000):9.
82: “Recycled Tires for a Building System”, 1999; Annual Form 10-KSB Report, The Quantum Group, Inc., 31 December 1998; Return Trip: How To Recycle the Family Car, 1994.
83: ” Solar Radiation Data Manual for Flat-Plate and Concentrating Collectors: 30-Year Average of Monthly Solar Radiation, 1961–1990, Spreadsheet Portable Data Files, DOE Renewable Resource Data Center.
84: George M. Hidy, The Winds: The Origins and Behavior of Atmospheric Motion, D. Van Nostrand Company, Princeton, NJ, 1967.
85: Evan R.C. Reynolds, Frank B. Thompson, eds., Forests, Climate, and Hydrology: Regional Impacts, United Nations University Press, Tokyo, Japan, 1988; see Effect of surface cover on land surface processes.
86: Map of roughness parameter due to vegetation in the U.K.
87: PSUBAMS Model, Dual roughness regimes, April 1997.
88: Horace Robert Byers, Synoptic and Aeronautical Meteorology, McGraw-Hill Book Company, New York, 1937.
89: Mindaugas Zickus, Influence of Meteorological Parameters on the Urban Air Pollution and its Forecast: Section 2.6.4 Vertical temperature gradient, Ph.D. Thesis, 1999.
90: Joseph Morgan, Introduction to University Physics, Volume One, Allyn and Bacon, Inc., Boston, MA, 1963.
91: Reporting on Climate Change: Understanding the Science. Chapter 3. Greenhouse Gases, Some Basics, Environmental Health Center, National Safety Council, Washington, DC, November 1994, ISBN 0–87912–177–7.
92: Robert J. Bradbury, personal communication, 8 May 2000.
93: B. Lobitz, L. Beck, A. Huq, B. Wood, G. Fuchs, A.S.G. Faruque, R. Colwell, Climate and infectious disease: Use of remote sensing for detection of Vibrio cholerae by indirect measurement, Proc. Natl. Acad. Sci. (USA) 97 (2000):1438–1443.
94: Shodor Education Foundation, Air Quality Meteorology, Session 5. Scales of Motion, 1996; Jet Stream Analyses and Forecasts at 300 mb.